Ghost Cell Pattern in MPI

Concept

Ghost cells refer to additional boundary cells that are replicated or exchanged between neighboring computational domains or processors.

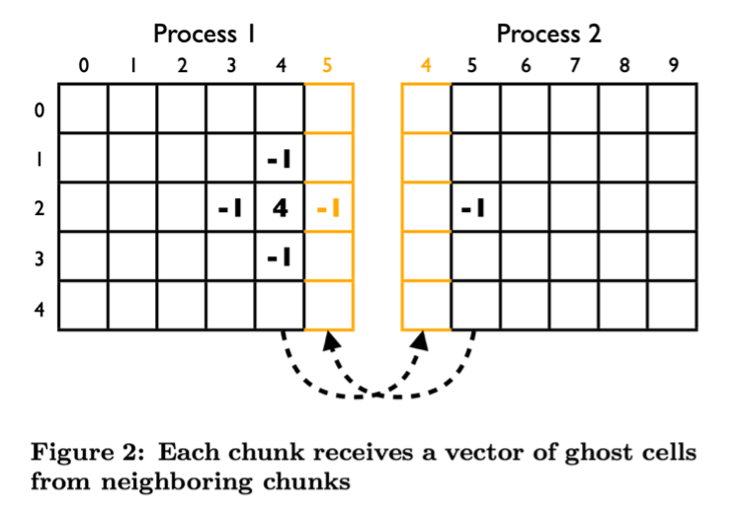
Data Exchange

Using MPI_Isend and MPI_Irecv synchronously for the exchange, so MPI_Waitall is needed to wait for the receiver to finish. Running a 3000x3000 matrix with 20 processes takes 34.5 seconds.

static void exchange(Solver* solver)
{
    MPI_Request requests[4] = { MPI_REQUEST_NULL,
        MPI_REQUEST_NULL,
        MPI_REQUEST_NULL,
        MPI_REQUEST_NULL };

    /* exchange ghost cells with top neighbor */
    if (solver->rank + 1 < solver->size) {
        int top     = solver->rank + 1;
        double* src = solver->p + (solver->jmaxLocal) * (solver->imax + 2) + 1;
        double* dst = solver->p + (solver->jmaxLocal + 1) * (solver->imax + 2) + 1;

        MPI_Isend(src, solver->imax, MPI_DOUBLE, top, 1, MPI_COMM_WORLD, &requests[0]);
        MPI_Irecv(dst, solver->imax, MPI_DOUBLE, top, 2, MPI_COMM_WORLD, &requests[1]);
    }

    /* exchange ghost cells with bottom neighbor */
    if (solver->rank > 0) {
        int bottom  = solver->rank - 1;
        double* src = solver->p + (solver->imax + 2) + 1;
        double* dst = solver->p + 1;

        MPI_Isend(src, solver->imax, MPI_DOUBLE, bottom, 2, MPI_COMM_WORLD, &requests[2]);
        MPI_Irecv(dst, solver->imax, MPI_DOUBLE, bottom, 1, MPI_COMM_WORLD, &requests[3]);
    }

    MPI_Waitall(4, requests, MPI_STATUSES_IGNORE);
}

But using MPI_Send and MPI_Recv for the matrix of the same size results in a runtime of 35.6 seconds.

Matrix Boundary

For example, using 4 processes to compute matrix 12x12, having 3 internal cells and 2 boundary cells in each cell, resulting in the following outcome from the solution provided in the exercise.

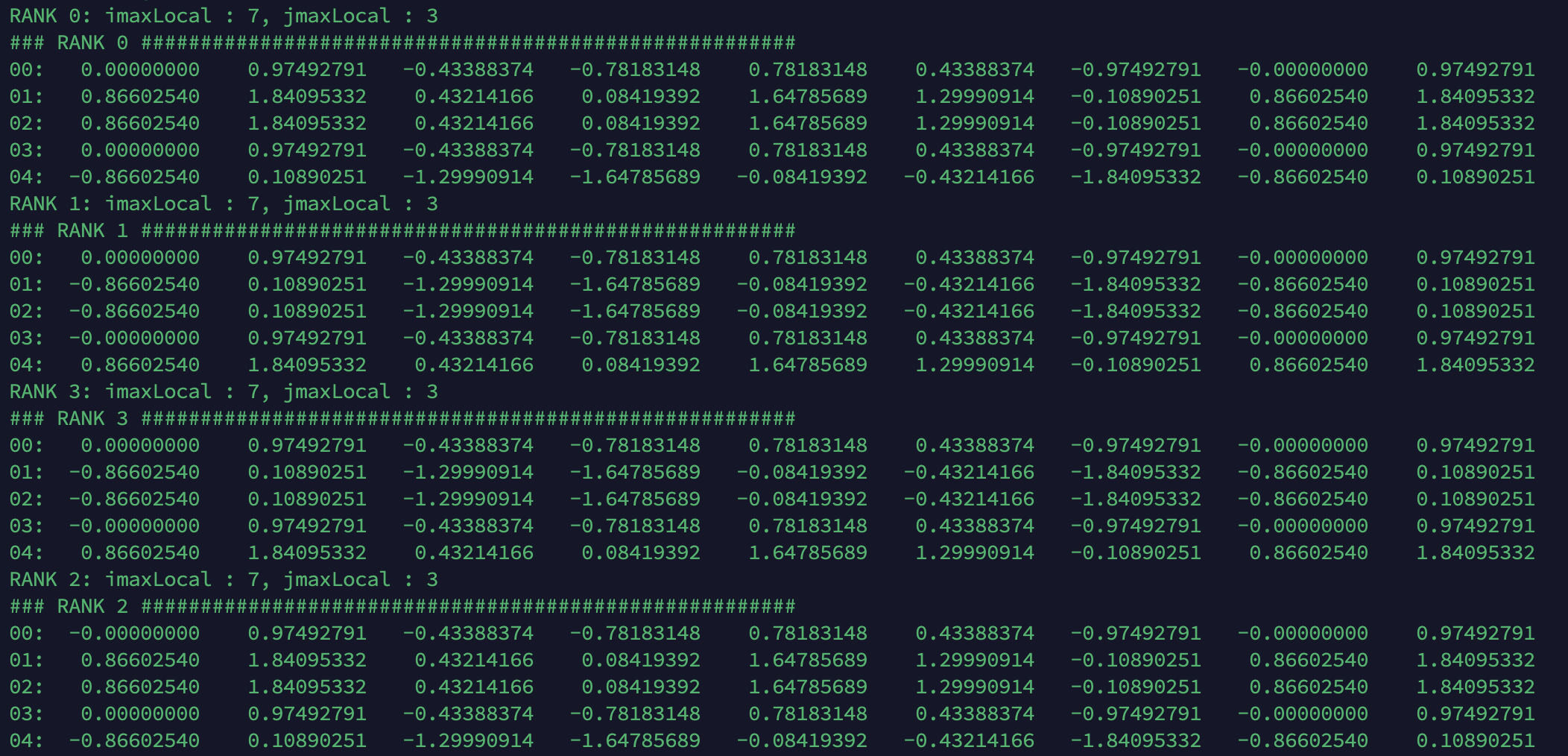
But in my solution, I made it a bit more complex by considering that the first-ranked process doesn’t need the top boundary for exchange, and the last-ranked process doesn’t need the bottom boundary. To handle this, I added some if conditions to determine the boundary requirements, which is also makes my exchange function more complex.

int boundaryRow = (solver->rank == 0 || solver->rank == solver->size-1) ? 1 : 2;

Here are my results below. I set all the exchange row values to 0, which makes the first updated result matrix(RHS matrix) a bit different initially. However, in the end, they’ll end up being the same.

Summarize

Even though the outcomes match the solution, I should strive to simplify the program as much as possible.

References

Ghost Cell Pattern